آموزش معادله خط
فهرست مطالب
فصل 6 ریاضی نهم - صفر تا صد معادله خط
معادله خط به یکی از دو شکل زیر نوشته میشود:
- فرم کلی \LARGE ax+by+c=o
- فرم استاندارد \LARGE y=mx+n
در فرم استاندارد \LARGE m را شیب خط و \LARGE n را عرض از مبدأ مینامند. قابل ذکر است که اگر یک معادله خط به فرم کلی نوشته شده باشد میتوان آن را به فرم استاندارد تبدیل کرد. به مثال زیر توجه کنید.
مثال 1.
شیب و عرض از مبدأ خط \LARGE3x+2y-4=0 را بهدست آورید.
برای حل این مثال ابتدا معادله خط دادهشده را به فرم استاندارد تبدیل میکنیم. برای این منظور لازم است \LARGE{y} سمت چپ معادله باشد و بقیه اجزاء به سمت راست منتقل شوند:
\LARGE2y=-3x+4
و سپس باید طرفین معادله را بر ضریب \LARGE{y} یعنی 2 تقسیم کنیم:
\LARGE{y=\frac{-3}{2}x+2}
یعنی با توجه به فرم استاندارد خواهیم داشت:
\LARGE{m=\frac{-3}{2}\ ,\ n=2}
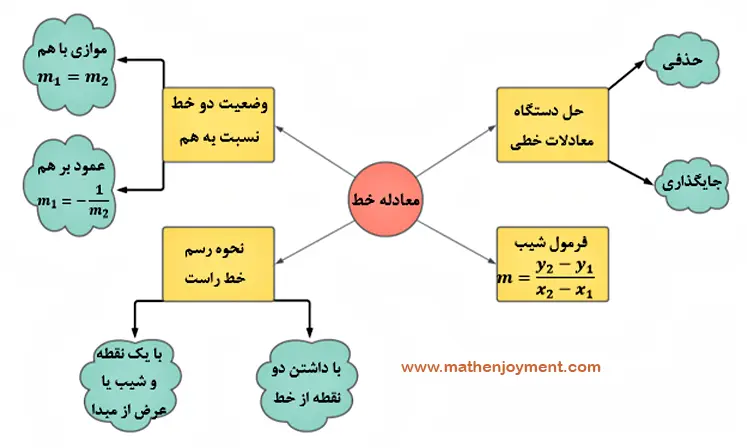
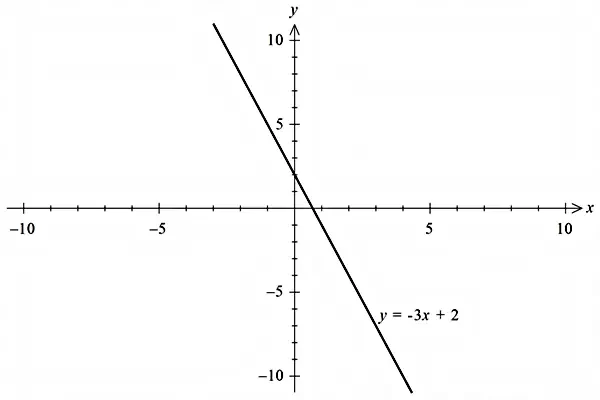
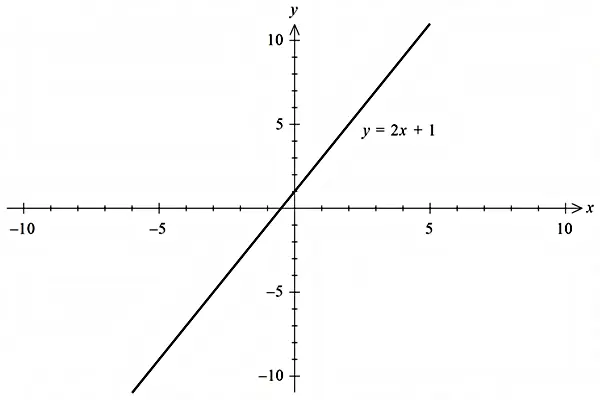
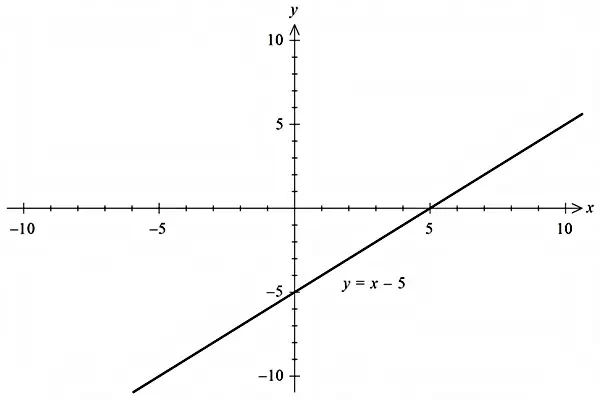
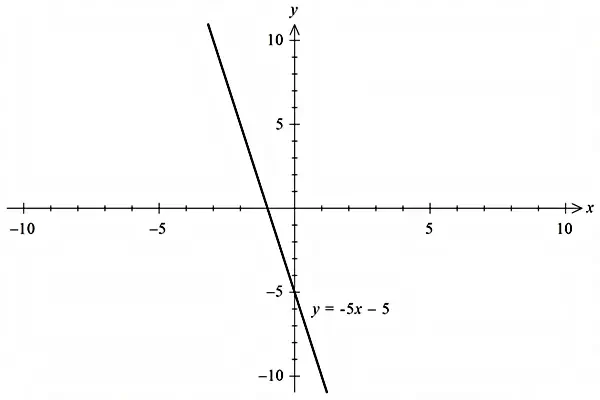
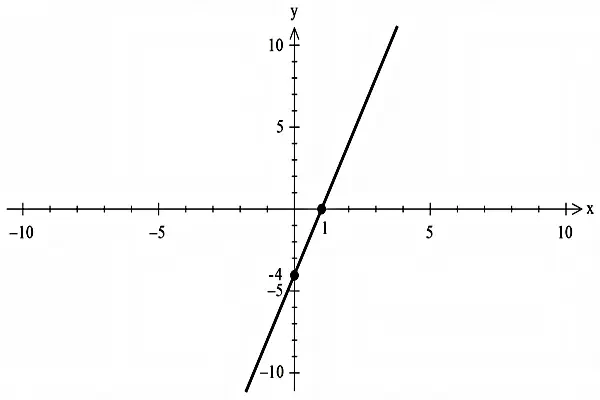
با توجه به اینکه شیب خط و عرض از مبدأ میتوانند اعدادی مثبت یا منفی باشند، خط راست میتواند شکل متفاوتی داشته باشد که میتوانید نمونههای آنرا در زیر ببینید:
همین حالا در آزمون آنلاین فصل 6 ریاضی نهم شرکت کنید.
در شکلهای بالا این نکته بهخوبی قابل مشاهده است که اگر در معادله خط، شیب مثبت باشد، خط رسم شده با جهت مثبت محور طولها زاویهای کمتر از نود درجه میسازد و اگر شیب منفی باشد، خط با جهت مثبت محور طولها زاویهای بیشتر از نود درجه تشکیل میدهد. لازم به ذکر است که محل تقاطع خط با محور عرضها را عرض از مبدأ مینامیم (برای مشاهده دقیقتر عکسها روی آنها کلیک کنید).
برای درک بیشتر مفهوم شیب خط میتوانید اینجا را ببینید.
خطهای خاص
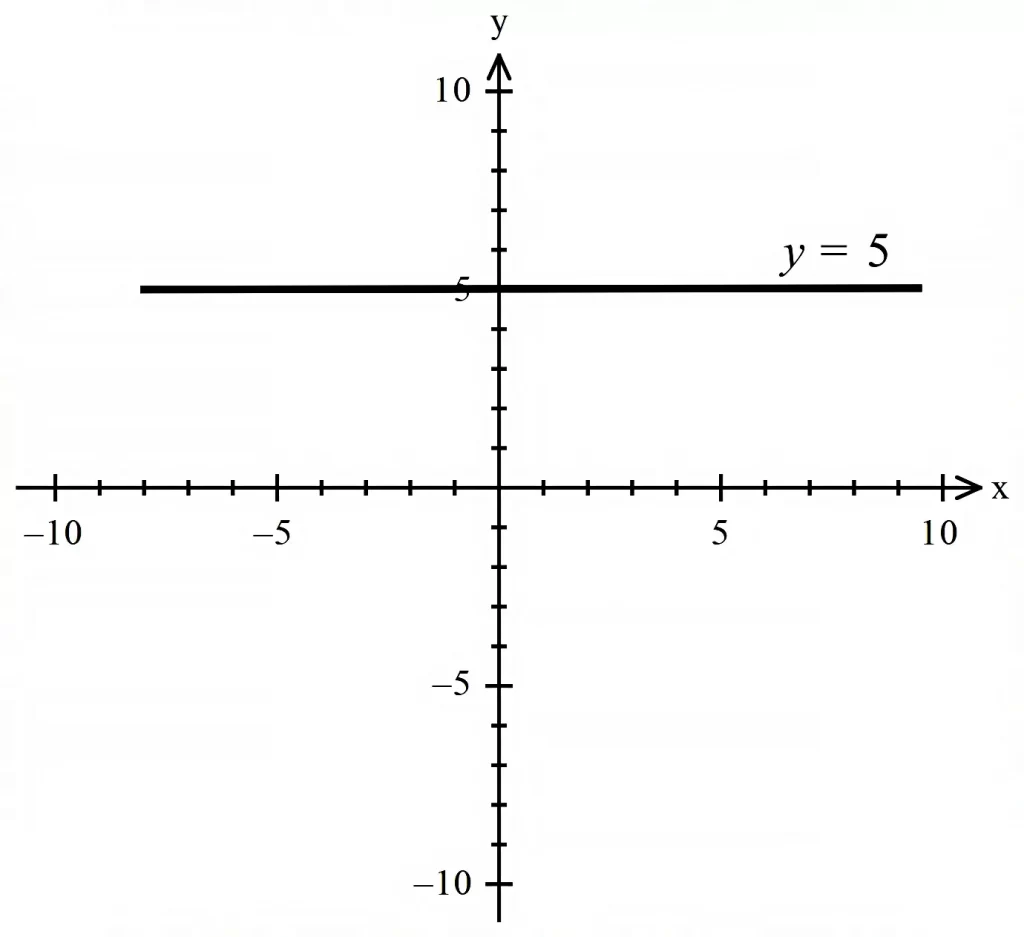
- خطوطی به فرم کلی \LARGE{y=b} که در آن \LARGE{b} یک عدد حقیقی است و شیب آنها صفر است و بهموازات محور طولها رسم میشوند.
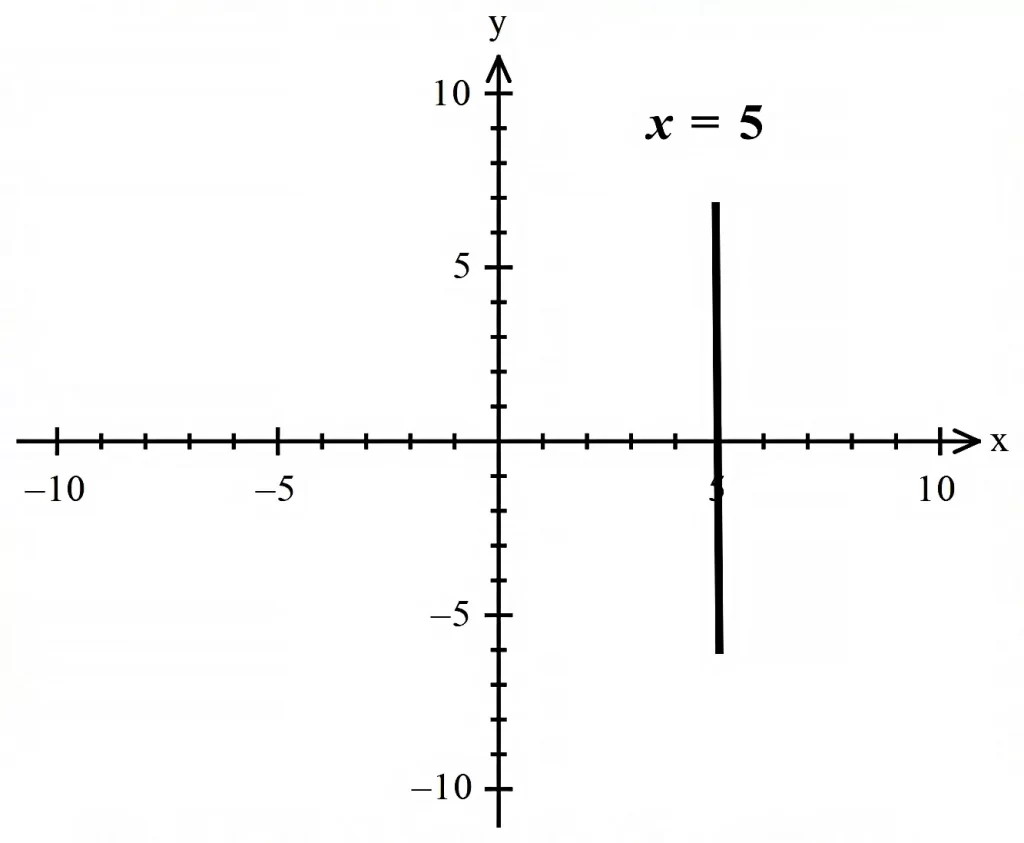
- خطوطی به فرم کلی \LARGE{x=a} که در آن \LARGE{a} یک عدد حقیقی است و شیب آنها بینهایت یا اصطلاحا تعریفنشده است و بهموازات محور عرضها رسم میشوند.
رسم خط راست با داشتن معادله خط
برای رسم خط راست با توجه به معادله خط داده شده کافیست بهصورت زیر پیش برویم:
میدانیم از یک نقطه بینهایت خط راست عبور میکند. اما از دو نقطه تنها یک خط منحصربفرد میگذرد. لذا برای اینکه بتوانیم یک خط راست را رسم کنیم کافیست حداقل دو نقطه از خط را داشته باشیم.
بهترین راه یافتن دو نقطه از خط این هست که محل تقاطع خط را با محور طولها و محور عرضها بهدست آوریم.
محل تقاطع با محور طولها نقطهای است که عرض آن صفر میباشد و محل تقاطع با محور عرضها نقطهای است که طول آن صفر است.
محل برخورد با محور طولها: \LARGE{\begin{bmatrix} x \\ 0 \end{bmatrix}}
(\LARGE{x} میتواند هر عددی باشد)
محل برخورد با محور عرضها: \LARGE{\begin{bmatrix} 0 \\y \end{bmatrix}}
(\LARGE{y} میتواند هر عددی باشد)
مثال 2. خط \LARGE{y=4x-4} را رسم کنید.
برای رسم خط مورد نظر ابتدا نقطه یابی انجام میدهیم (یکبار طول را صفر میهیم و عرض را بهدست میآوریم و بالعکس):
| y | x |
|---|---|
| 4- | 0 |
| 0 | 1 |
بهدست آوردن معادله خط با استفاده از دو نقطهی داده شده
همانطور که در قسمت قبل اشاره کردیم برای اینکه معادله یک خط را بهدست آوریم کافیست حداقل دو نقطه از خط را داشته باشیم. سپس روند زیر را در پیش میگیریم:
هر خط راست دو مشخصهی بارز دارد: شیب و عرض از مبدأ. پس در ابتدا باید بدانیم چگونه میتوان بهوسیلهی دو نقطهی A و B این دو مقدار اصلی را بهدست آورد. مختصات نقاط A و B را بهصورت زیر در نظر میگیریم:
\LARGE{A=\begin{bmatrix} x_A \\ y_A\end{bmatrix}}\, ,\, \LARGE{B=\begin{bmatrix} x_B \\ y_B\end{bmatrix}}
حال ابتدا از فرمول زیر شیب خط یعنی \LARGE{m} را محاسبه میکنیم:
\LARGE{m=\frac{y_A-y_B}{x_A-x_B}}
معادله خط را بهصورت استاندارد زیر در نظر میگیریم:
\LARGE{y=mx+n}
و یکی از نقاط A یا B را انتخاب کرده و مختصات آن نقطه را بجای \LARGE{x} و \LARGE{y} در فرمول بالا قرار میدهیم و مقدار مجهول \LARGE{n} را بهدست میآوریم. توجه داریم که مقدار \LARGE{m} را نیز از فرمول بالا محاسبه کردهایم.
برای درک بیشتر مفاهیم بالا به حل یک مثال میپردازیم.
مثال3.
معادلهی خطی که از دو نقطهی زیر میگذرد را بهدست آورید.
\LARGE{A=\begin{bmatrix}2 \\ -3\end{bmatrix}}\, ,\, \LARGE{B=\begin{bmatrix} 1 \\ 0\end{bmatrix}}
ابتدا شیب خط را از فرمول زیر بهدست میآوریم:
\LARGE{m=\frac{y_A-y_B}{x_A-x_B}=\frac{-3-0}{2-1}=-3}
حال طبق توضیحات قبل کافیست یکی از نقاط A یا B را بهدلخواه انتخاب کنیم. مثلا نقطه A را در نظر میگیریم و طول و عرض آن را در معادلهی زیر قرار میدهیم:
\LARGE{x_A=2\, ,\,y_A=-3}
\LARGE{y=mx+n\, ,\, -3=(-3)(2)+n}
و در نتیجه خواهیم داشت:
\LARGE{n=3}
و به این ترتیب معادله خط مورد نظر بهصورت زیر خواهد بود:
\LARGE{y=-3x+3}
مثال 4.
آیا نقطهی \LARGE{A=\begin{bmatrix} 2\\ -1 \end{bmatrix}} روی خط \LARGE{y=3x-1} قرار دارد یا خیر؟
برای تحقیق این موضوع کافیست طول نقطهی داده شده را در معادله خط مورد نظر قرار دهیم و ببینیم آیا عرض هم همان عدد 1- بهدست میآید یا خیر. اگر 1- بود یعنی این نقطه روی خط مورد نظر قرار دارد و بهعبارتی دیگر خط مذکور از نقطه عبور میکند.
\LARGE{y=3x-1}
ینی نقطهی مورد سؤال روی خط قرار ندارد.
فاصله بین دو نقطه A و B یا طول پاره خط AB
فرض کنید دو نقطه با مختصات \LARGE{A=\begin{bmatrix} x_1 \\ y_1 \end{bmatrix}} و \LARGE{B=\begin{bmatrix} x_2 \\ y_2 \end{bmatrix}} را داریم. فاصله بین دو نقطه در واقع طول پاره خط واصل بین آنها است. طول این پاره خط از فرمول زیر بهدست میآید:
\LARGE{|AB|=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}}
(طول پاره خط AB را با نماد \LARGE{|AB|} نمایش میدهیم).
مثال5.
طول پاره خط واصل بین دو نقطهی \LARGE{A=\begin{bmatrix} -1 \\ 0 \end{bmatrix}} و \LARGE{B=\begin{bmatrix} 2 \\ 4 \end{bmatrix}} را بهدست آورید.
از فرمول زیر استفاده میکنیم:
\LARGE{|AB|=\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}}
\LARGE{=\sqrt{(2-(-1))^2+(4-0)^2}}
\LARGE{=\sqrt{16+9}=5}
مختصات نقطه وسط پاره خط AB
دو نقطه با مختصات \LARGE{A=\begin{bmatrix} x_1 \\ y_1 \end{bmatrix}} و \LARGE{B=\begin{bmatrix} x_2 \\ y_2 \end{bmatrix}} را در نظر بگیرید. مختصات نقطهای مانند \LARGE{M=\begin{bmatrix} x_M \\ y_M \end{bmatrix}}، وسط پارهخط AB بهصورت زیر بهدست میآید:
\LARGE\begin{cases}x_M=\frac{x_1+x_2}{2} \\y_M=\frac{y_1+y_2}{2}\end{cases}
مثال 6.
در مثال قبل مختصات نقطه وسط پارهخط AB را محاسبه نمایید.
\LARGE\begin{cases}x_M=\frac{x_A+x_B}{2} \\y_M=\frac{y_A+y_B}{2}\end{cases}
\LARGE\begin{cases}x_M=\frac{-1+2}{2} \\y_M=\frac{0+4}{2}\end{cases}
\LARGE\begin{cases}x_M=\frac{1}{2} \\y_M=2\end{cases}
فاصله یک نقطه از یک خط
نقطهای با مختصات \LARGE{A=\begin{bmatrix} x_0 \\ y_0 \end{bmatrix}} را در نظر بگیرید. فرمول محاسبهی فاصله نقطهی مورد نظر از خط \LARGE{ax+by+c=0} بهصورت زیر است:
\LARGE{\frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}}
نکته مهم: شرط استفاده از فرمول بالا این است که معادله خط موردنظر حتما باید به فرم کلی باشد. اگر معادله خط به صورت استاندارد بود تمام اجزاء را به یک طرف معادله میبریم تا به فرم کلی تبدیل شود.
دستگاه معادلات دومجهولی
معادله خط و دستگاه معادلات دومجهولی دو مبحث جدانشدنی هستند و هر یک مکمل دیگری است. دلیل آن هم این است که یک دستگاه معادلات دومجهولی از دو معادله تشکیل شده است که هر کدام از آنها معادلهی خط منحصربفردی هستند. این خطوط منحصربفرد میتوانند متقاطع، موازی و در فضای بیش از دو بعد، متنافر نیز باشند.
روش حل دستگاه معادلات دومجهولی با روش حذفی
برای استفاده از این روش گامهای زیر را دنبال میکنیم:
- ابتدا لازم است که معادلات مرتب شوند. به این معنی که \LARGE{x} ها و \LARGE{y} ها زیرهم نوشته شوند.
- به ضرایب اولین متغیرمان توجه میکنیم. معادله اول را در ضریب متغیر پایینی ضرب میکنیم و معادله دوم را در قرینهی ضریب متغیر بالایی ضرب میکنیم (یا بالعکس)
- سپس هر دو معادله را با هم جمع میکنیم و یک معادلهی یک مجهولی بهدست میآید که از طریق آن مقدار مجهول محاسبه میشود.
- حال مقدار بهدست آمده را در یکی از معادلات اولیه قرار میدهیم (کاملا دلخواه) و مجهول دیگر را نیز بهدست میآوریم.
مثال 7.
دستگاه معادلات دومجهولی زیر را حل کنید و وضعیت دو خط را نسبت به هم بررسی کنید.
\LARGE\begin{cases}x-2y=3 \\2x-y=3\end{cases}
گام اول.
معادلهها مرتب شده هستند(\LARGE{x} ها و \LARGE{y} ها زیرهم نوشته شدهاند)
گام دوم.
ضریب \LARGE{x} بالایی 1 و ضریب \LARGE{x} پایینی 2 است. معادله بالا را در 2- و معادله پایین را در 1 ضرب میکنیم:
\LARGE\begin{cases}-2x+4y=-6\\2x-y=3\end{cases}
گام سوم.
حال طرفین دو معادله بالا را با هم جمع میکنیم. \LARGE{2x} و \LARGE{-2x} که قرینه هم هستند و با هم حذف میشوند و لذا خواهیم داشت:
\LARGE{3y=-3}
\LARGE{y=-1}
گام چهارم.
و با قرار دادن مقدار \LARGE{y} بهدست آمده در یکی از معادلات داده شده در ابتدای سؤال، مقدار \LARGE{x} را نیز بهدست میآوریم:
\LARGE{x-2y=3}\LARGE{x-2(-1)=3}\LARGE{x=1}
یعنی نقطهی \LARGE{A=\begin{bmatrix} 1\\ -1 \end{bmatrix}} جواب دستگاه معادلات دو مجهولی دادهشده است. در واقع این نقطه محل برخورد دو خط مفروض است. یا بهعبارتی دو خط متقاطع هستند.
(دقت داشته باشید هرگاه دستگاه معادلات خطی دو مجهولی یک جواب منحصربفرد داشته باشد، که یک نقطه است، مختصات آن در معادلهی هر دو خط صدق میکند. یعنی هر دو خط از نقطهی مذکور عبور میکنند)
تمرین زیر را حل کنید و پاسخ آن را برایمان ارسال بفرمایید.
تمرین .
برای اطمینان از اینکه روش را بهخوبی یاد گرفتهاید تمرین زیر را حل کنید و پاسخ را برایمان ارسال کنید.
\LARGE\begin{cases}3x+y=2 \\x-2y=3\end{cases}
حل دستگاه معادلات خطی دو مجهولی با روش جایگذاری
در این روش کافیست یکی از معادلات خطی داده شده را به دلخواه انتخاب کنیم و \LARGE{x} را بر حسب \LARGE{y} بهدست آوریم یا بالعکس. سپس بجای \LARGE{x} در معادله دوم مقدار محاسبه شده از گام اول را قرار دهیم. با این اقدام یک معادلهی درجه اول بر حسب \LARGE{y} داریم که مقدار \LARGE{y} را از آن بهدست آورده سپس در معادله اول قرار میدهیم و \LARGE{x} را هم بهدست میآوریم.
مثال 8.
حال میخواهیم تمرین 1 را از روش جایگذاری حل کنیم.
\LARGE\begin{cases}3x+y=2 \\x-2y=3\end{cases} از معادلهی اول خواهیم داشت:
\LARGE{3x=2-y}
\LARGE{x=\frac{2-y}{3}}
حال مقدار \LARGE{x} بهدست آمده را در معادلهی دوم جایگذاری میکنیم:
\LARGE{x-2y=3}
\LARGE{\frac{2-y}{3}-2y=3}
\LARGE{-7y+2=9}
\LARGE{y=-1}
در این مرحله کافیست یکی از معادلات دستگاه را به دلخواه انتخاب کرده و مقدار \LARGE{y} را در آن قرار دهیم و \LARGE{x} را محاسبه کنیم که پس از انجام این کار خواهید دید \LARGE{x=1} و جواب دقیقا همان مقادیر تمرین قبل میباشد.
مثال 9.
وضعیت دو خط \LARGE{y=-2x+3} و \LARGE{y=\frac{1}{2}x-1} را نسبت به هم بررسی کنید.
همانطور که مشخص است شیب خط اول برابر است با \LARGE{m=-2} و شیب خط دوم برابر است با \LARGE{m’=\frac{1}{2}} و خواهیم داشت:
\LARGE{m×m’=-1}
لذا نتیجه میگیریم دو خط مورد نظر بر هم عمودند.
وضعیت دو خط نسبت به هم
برای تشخیص وضعیت دو خط نسبت به هم باید به دنبال حل دستگاه معادلات دومجهولی داده شده باشیم. دستگاه زیر را در نظر میگیریم:
\LARGE\begin{cases}ax+cy=m \\bx+dy=n\end{cases}
بعد از حل دستگاه معادلات دومجهولی یکی از حالتهای زیر رخ میدهد:
- دستگاه یک جواب منحصربفرد دارد که در این حالت میگوییم دو خط متقاطع هستند و این معادل است با اینکه:\LARGE\frac{a}{b}≠\frac{c}{d}
- دستگاه بیشمار جواب دارد لذا پی میبریم که دو خط بر هم منطبق هستند و بهعبارتی رابطهی زیر برقرار است: \LARGE\frac{a}{b}=\frac{c}{d}=\frac{m}{n}
- دستگاه اصلا جواب ندارد و به این معنی است که دو خط با هم موازی هستند و یعنی:\LARGE\frac{a}{b}=\frac{c}{d}≠\frac{m}{n}
نکته
اگر معادلهی دو خط به فرم استاندارد باشد، یعنی \LARGE y=mx+n و \LARGE{y=m’x+n’} که در آن \LARGE{m} شیب خط اول و \LARGE{m’} شیب خط دوم است، اگر:
- \LARGE{m=m’} دو خط با هم موازی هستند.
- \LARGE{m×m’=-1} دو خط بر هم عمودند.
مشق شب برای شما
مشق اول .
وضعیت خطهای زیر را نسبت به هم بررسی کنید.
\Large\begin{cases}x+y=1 \\ 2x+2y=5\end{cases}
\Large\begin{cases}x-2y=-3 \\ 3x-6y=-9\end{cases}
مشق دوم .
مقدار \Large{m} را چنان تعیین کنید که دو خط زیر با هم موازی باشند.
\Large\begin{cases}(m-1)x+my=1 \\4mx+(m-1)y=-2\end{cases}
مشق سوم .
معادلهی خطی را بنویسید که از نقطهی \Large{A(-3,2)} بگذرد و با خط \Large{2x-4y=3} موازی باشد.
اگر در حل این سؤالات یا بطور کلی در یادگیری مبحث معادله خط و حل دستگاه معادلات دو مجهولی با چالش مواجهید برای بهره بردن از کلاسهای خصوصی آنلاین در سراسر کشور یا خارج از ایران و کلاسهای حضوری ویژهی مشهد با ما تماس بگیرید.
سلام ممنون از مقاله مفید شما
زنده باشید