تدریس سهمی دهم ریاضی تجربی جزء آموزشهای درسی بسیار چالشانگیز و مهم است که ما مدرسین ریاضی باید توجه ویژهای به آن داشته باشیم.
مبحث سهمی ارتباط کاملا مستقیمی با معادلات درجه دوم دارد. لذا توصیه میکنم قبل از پرداختن به یادگیری سهمی تسلط نسبتا خوبی در معادلات درجه ۲ کسب نمایید. بهعبارتی، سهمی، نمودار متناظر با یک رابطه درجه دو است.
به این منظور پیشنهاد من این است که مقالهی روش های حل معادله درجه دو را ابتدا با دقت مطالعه فرمایید.
آنچه در این مقاله میخوانید:
سهمی
محور تقارن سهمی
رسم سهمی
رأس سهمی
عرض از مبدأ
طول از مبدأ
تدریس سهمی دهم و معادلات درجه دوم
همانطور که میدانید فرم کلی معادله درجه دو بهصورت (\(\large a≠0\)) ، \(\large ax^2+bx+c=o\) است. حال اگر در معادله بالا بهجای عدد صفر \(\large y\) قرار گیرد، معادله سهمی بهصورت \(\large y=ax^2+bx+c\) بهدست میآید.
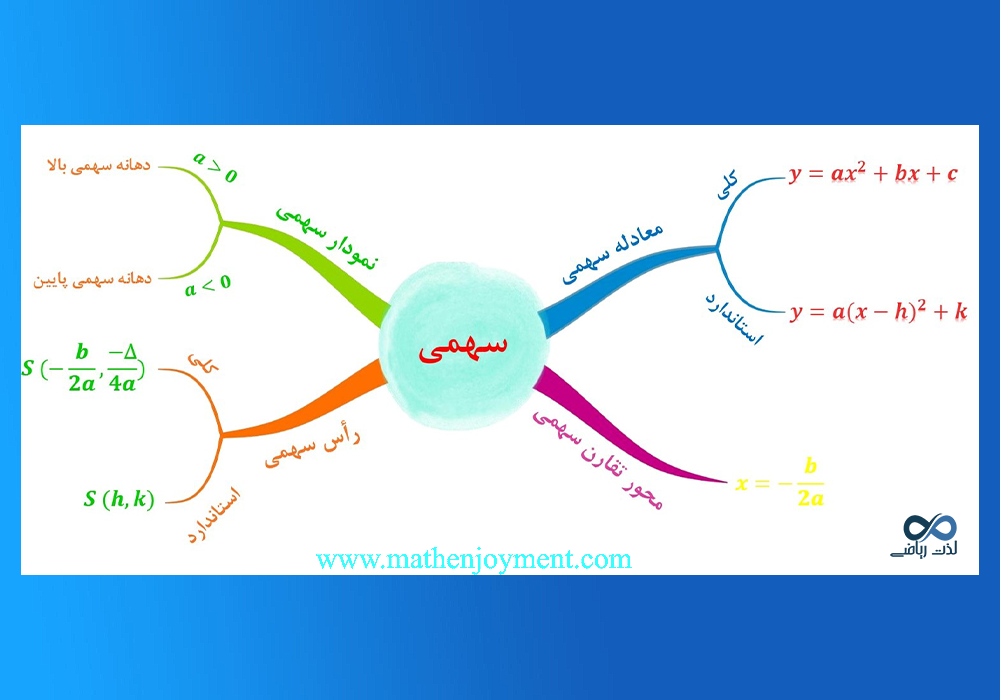
معادله سهمی به دو صورت کلی و استاندارد وجود دارد:
- فرم کلی \(\large y=ax^2+bx+c\)
- فرم استاندارد \(\large y=a(x-h)^2+k\)
مختصات رأس سهمی
رأس سهمی مهمترین مشخصهی آن است و نقطهای است که نمودار سهمی نسبت به آن متقارن است. برای یافتن مختصات رأس سهمی با توجه به اینکه معادله سهمی به فرم کلی یا استاندارد باشد به دو شیوهی زیر عمل میکنیم:
یکی از بهترین کارهایی که میشه انجام داد، کمک به افزایش آگاهی و دانش دیگران هست. مثلا میتونید کتابهای درسی و کمک درسی که مربوط به سالهای گذشته هستن و نیازی بهشون ندارید رو به دانشآموزانی که توانایی خرید این کتابها رو ندارن تقدیم کنید.
در هر شهری که زندگی میکنید مراکزی برای دریافت کتابها وجود دارن. کافیه با یک سرچ ساده در گوگل اونها رو پیدا کنید.
یافتن مختصات رأس سهمی در حالت کلی
سهمی با معادلهی \(\large y=ax^2+bx+c\) را در نظر میگیریم. رأس سهمی را با \(\large S\) نمایش میدهیم. بهمنظور محاسبه مختصات \(\large S\) ابتدا طول آن را از فرمول زیر محاسبه میکنیم:
\[\large{x_s=\frac{-b}{2a}}\]
محاسبهی \(\large y_s\) را به دو روش میتوان انجام داد:
روش اول. \(\large x_s\) را که از مرحلهی قبل محاسبه کردیم در معادلهی \(\large y=ax^2+bx+c\) بجای \(\large x\)ها قرار میدهیم. مقداری که برای \(\large y\) بهدست میآید همان \(\large y_s\) است.
روش دوم. از فرمول \[\large{y_s=\frac{-Δ}{4a}}\] استفاده میکنیم. در این فرمول:
\[\large{Δ=b^2-4ac}\]
مثال ۱) مختصات رأس سهمی \(\large y=3x^2-6x+1\) را بهدست آورید.
حل: ابتدا مقدار \(\large x_s\) را محاسبه میکنیم: \[\large{x_s=\frac{-b}{2a}}\]
\[\large{x_s=\frac{6}{6}=1}\]
حال \(\large y_s\) را از هر دو روش بهدست میآوریم تا کاملا مشاهده کنیم مقدار یکسانی برای آن بهدست میآید.
روش اول: مقدار \(\large x_s=1\) را در معادلهی \(\large y=3x^2-6x+1\) بهجای \(\large x\)ها قرار میدهیم:
\[\large{y=3(1)^2-6(1)+1=-2}\]
یعنی: \(\large y_s=-2\)
روش دوم: ابتدا مقدار \(\large Δ\) را بهصورت زیر محاسبه میکنیم: \[\large{Δ=b^2-4ac}\]
\[\large{Δ=(-6)^2-4(3)(1)}\]
\[\large{Δ=24}\]
حال با توجه به فرمول روش دوم داریم:
\[\large{y_s=\frac{-Δ}{4a}=\frac{-24}{4(3)}=-2}\]
همانطور که مشاهده کردید از هر دو روش مقدار یکسانی برای \(\large y_s\) بهدست آمد.
حال میتوان مختصات رأس سهمی را بهصورت زیر نمایش داد:
\[\large{S (1,-2)}\]
همین حالا در آزمون آنلاین سهمی دهم شرکت کنید.
یافتن رأس سهمی از معادله استاندارد سهمی
همانطور که قبلا اشاره کردیم معادله استاندارد سهمی بهصورت \(\large y=a(x-h)^2+k\) میباشد. در این حالت مختصات رأس سهمی برابر است با:
\[\large{S (h,k)}\]
باید به این نکتهی بسیار مهم توجه کنیم که تنها در صورتی مختصات رأس سهمی بهصورت \(\large S (h,k)\) است که در معادله استاندارد سهمی یعنی \(\large y=a(x-h)^2+k\) حتما داخل پرانتز بین \(\large x\) و \(\large h\) علامت منفی و قبل از \(\large k\) علامت مثبت باشد. در غیر اینصورت با اعمال یک ترفند خودمان معادله را به فرم مورد نظر تبدیل میکنیم.
مثال های مختصات رأس سهمی در حالت استاندارد
مثال ۲) مختصات رأس سهمی \(\large y=3(x-2)^2+3\) را بهدست آورید.
حل: بر اساس شکل استاندارد معادله سهمی در این مثال \(\large h\) برابر ۲ و \(\large k\) برابر است با ۳. (توجه داریم که نکته مهمی که در قسمت قبل با رنگ قرمز نوشته شده در مورد این مثال صدق میکند). لذا مختصات رأس سهمی در اینجا برابر است با: \(\large S(2,3)\)
مثال ۳) مختصات رأس سهمی \(\large y=-(x+4)^2-1\) را بهدست آورید.
حل: معادله سهمی در حالت استاندارد بهصورت \(\large y=a(x-h)^2+k\) است. اگر به سهمی داده شده در این مثال دقت کنید بهخوبی مشخص است که ظاهرا شرایط مورد نظر حالت استاندارد را ندارد!
در واقع بین \(\large x\) و \(\large h\) بجای علامت منفی علامت مثبت است و همچنین قبل عدد یک باید علامت مثبت باشد! یعنی معادله داده شده نمیتواند معادله سهمی باشد؟! بدون شک این معادله یک سهمی را نمایش میدهد. برای دریافت چگونگی به ادامه حل دقت کنید:
معادله \(\large y=-(x+4)^2-1\) را به صورت زیر مینویسیم:
\[\large{y=-(x-(-4))^2+(-1)}\]
یعنی خودمان با ترفندی ساده معادله سهمی را طوری نوشتیم که به حالت استاندارد اصلی تبدیل شود. حال مقدار \(\large h\) عدد ۴- است نه ۴! همچنین مقدار \(\large k\) عدد ۱- است نه ۱. در نتیجه : \(\large S (-4,-1)\) .
میتوانید مقالهی تعیین علامت و نامعادله ریاضی دهم را از اینجا مطالعه کنید. (بههمراه ویدئوی آموزشی)
رسم سهمی
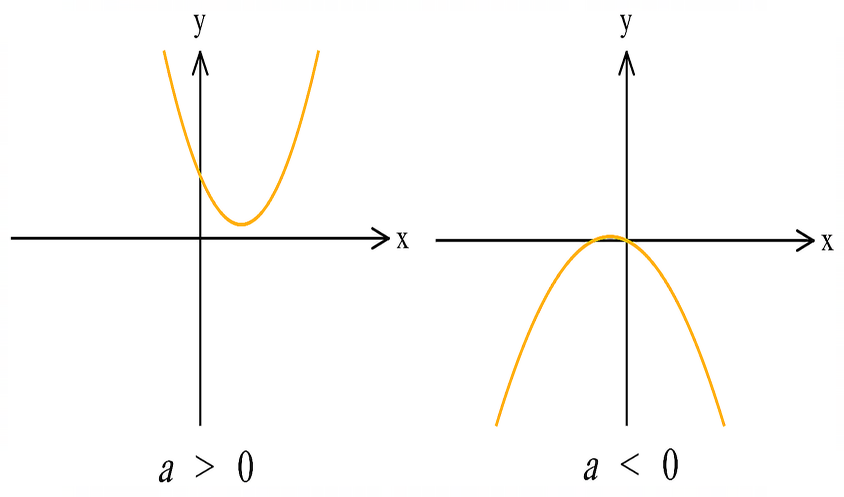
اولین گام جهت رسم سهمی توجه به این موضوع است که چه در حالت استاندارد معادله سهمی و نیز در فرم کلی، علامت متغیر \(\large a\) تعیین میکند که دهانه سهمی رو به بالا یا پایین است.
اگر \(\large a>0\) دهانه سهمی رو به بالا است (سهمی دارای نقطه مینیمم یا کمترین مقدار است). اگر \(\large a<0\) دهانه سهمی رو به پایین است (سهمی دارای نقطه ماکزیمم یا بیشترین مقدار است). به شکلهای زیر توجه کنید.
دومین گام، یافتن مختصات رأس سهمی است. حال باید طول از مبدأ و عرض از مبدأ را بیابیم. طول از مبدأ نقاطی هستند که نمودار تابع محور \(\large x\)ها را در آن نقاط قطع میکند. برای یافتن طول از مبدأ یک نمودار کافی است بجای \(\large y\) عدد صفر قرار دهیم.
مقادیر بهدست آمده برای \(\large x\)ها طول از مبدأ نمودار موردنظر هستند. بالعکس، عرض از مبدأ نقطهای است که نمودار تابع (که در اینجا تابع ما سهمی است) محور عرضها را در آن قطع میکند.
پس بدیهی است برای یافتن آن باید اینبار بهجای \(\large x\)ها مقدار صفر را قرار داده و \(\large y\) بهدست آمده عرض از مبدأ نمودار است.
با کمی دقت در معادله کلی سهمی یعنی \(\large y=ax^2+bx+c\) درمییابیم عرض از مبدأ نمودار سهمی مقدار متغیر \(\large c\) است. (کافی است بجای \(\large x\)ها مقدار صفر قرار دهیم).
حال کافیست دو نقطهی دیگر در طرفین رأس بیابیم. بهتر است این نقاط در یک فاصله از رأس قرار داشته باشند. چون نمودار سهمی نسبت به رأس خود متقارن است، لذا اگر دو نقطه در طرفین رأس به یک فاصله از آن باشند عرض یکسان دارند.
برای درک مطلب به مثالهای زیر دقت کنید.
مثال4) سهمی \(\large y=3(x-2)^2+3\) را رسم کنید.
حل: با توجه به اینکه معادله به شکل استاندارد است داریم: \(\large h=2\) و \(\large k=3\) . بنابراین \(\large S (2,3)\).
توجه داریم که فرم استاندارد سهمی بهصورت: \(\large y=a(x-h)^2+k\) است. همچنین \(\large a=3>0\) در نتیجه دهانه سهمی رو به بالاست.
حال به نقطهیابی میپردازیم. همانطور که ذکر کردیم کافیست دو نقطه در طرفین \(\large S\) پیدا کنیم.
در معادله سهمی داده شده یکبار بهجای \(\large x\) عدد 0 را قرار دهیم و مقداری که برای \(\large y\) بهدست میآید، 15 است. یکبار هم بهجای \(\large x\) عدد 4 را قرار داده و باز هم مقدار \(\large y\) عدد 15 خواهد بود.
| y | x |
|---|---|
| 15 | 0 |
| 3 | 2 |
| 15 | 4 |
با داشتن این سه نقطه یعنی: \(\large (0,15)\) ، \(\large (2,3)\) و \(\large(4,15)\) نمودار سهمی را بهصورت زیر رسم میکنیم:
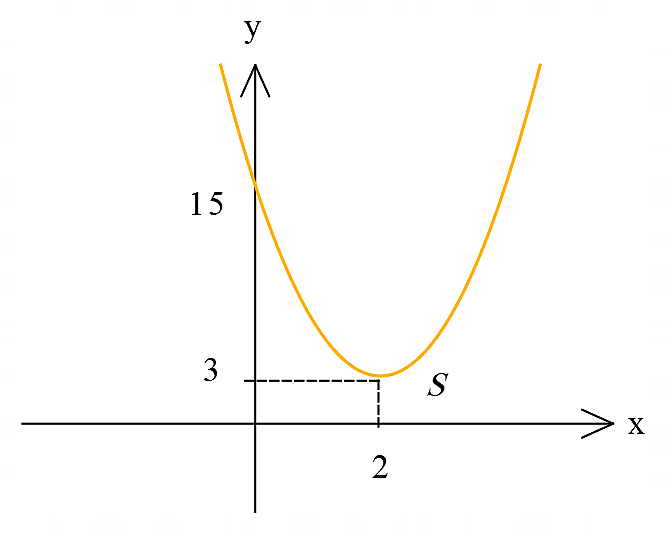
محور تقارن سهمی
محور تقارن سهمی قائم، خطی است که به موازات محور عرضها رسم میشود. معادله خط تقارن سهمی به صورت \(\large x=x_s\) است. \(\large x_s\) در واقع طول نقطه رأس سهمی است. همانطور که در مقاله آموزش معادله خط بیان کردیم یکی از خطهای خاص، خط به معادله \(\large x=a\) است که قائم است (موازی محور عرضها) و شیب آن تعریف نشده (بینهایت) است. جهت یادآوری میتوانید به مقاله آموزش معادله خط مراجعه کرده و از فهرست مطالب عنوان خطهای خاص را مطالعه بفرمایید.
ارتباط سهمی و معادله درجه دو
همانطور که از قبل میدانید برای معادلهی درجه دو \(\large ax^2+bx+c=0\) سه حالت رخ میدهد:
- \(\large Δ>0\)، معادله دارای دو ریشهی حقیقی و متمایز است.
- \(\large Δ=0\)، معادله دارای یک ریشه مضاعف است.
- \(\large Δ<0\)، معادله ریشهی حقیقی ندارد.
در ابتدای مقاله این موضوع را بیان کردیم که سهمی شکل نموداری معادله درجه دو است. این بدان معنی است که در واقع میخواهیم بدانیم که \(\large y\) در چه نقاطی صفر میشود. بهتر است بگوییم \(\large y\) در چه نقاطی محور \(\large x\) ها را قطع میکند.
- اگر معادله درجه دوم دو ریشه داشته باشد، نمودار سهمی محور \(\large x\) ها را در دو نقطه قطع میکند. مثالی برای این حالت در شکل زیر قابل مشاهده است:
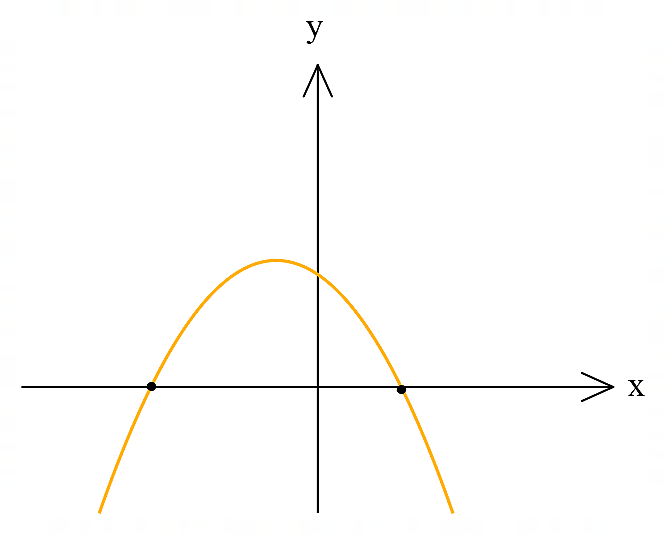
- اگر معادله درجه 2 تنها یک ریشه مضاعف داشته باشد، سهمی محور طولها را در یک نقطه قطع میکند. اصطلاحا بر محور طولها مماس است. یک مثال از این حالت را در ادامه ببینید:
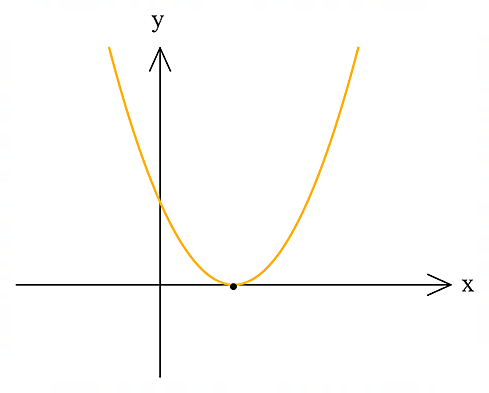
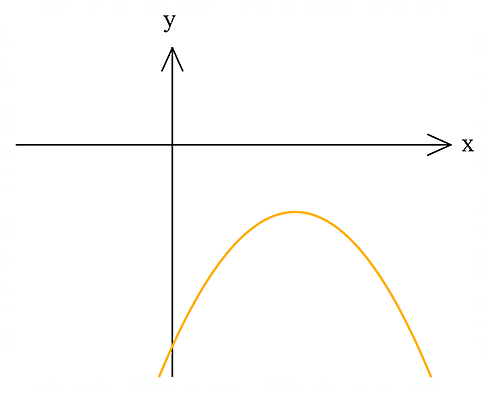
- اگر معادله درجه دوم ریشهی حقیقی نداشته باشد، محور طولها را در هیچ نقطهای قطع نمیکند. بهعبارتی یا بالای محور \(\large x\)ها ست یا پایین محور \(\large x\)ها. یک مثال آن را میتوانید در ادامه مشاهده کنید:
این مقاله را با دیگران به اشتراک بگذارید:
نکته بسیار مهم و کنکوری
معادله هر سهمی که محور \(\large x\)ها را در دو نقطه به طولهای \(\large x_1\) و \(\large x_2\) قطع کند بهصورت \(\large y=a(x-x_1)(x-x_2)\) است. همچنین معادلهی هر سهمی که در نقطهای به طول \(\large x_1\) بر محور \(\large x\) ها مماس است به شکل \(\large y=a(x-x_1)^2\) است.
مثال5) سهمی بهمعادلهی \(\large y=ax^2+bx+c\) بهصورت زیر است. \(\large a\) را بهدست آورید.
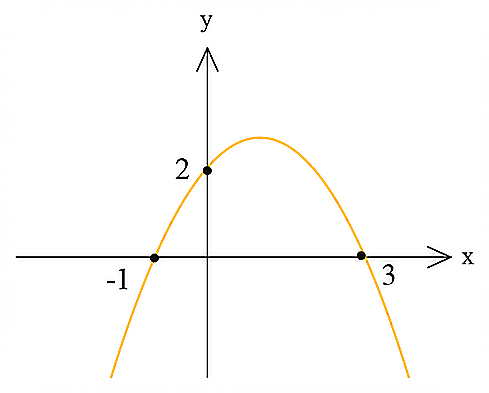
حل: با توجه به نکته قبل میتوان معادله سهمی را به صورت \(\large y=a(x-x_1)(x-x_2)\) نوشت. همانطور که از روی نمودار مشخص است، سهمی محور \(\large x\) را در دو نقطه \(\large x_1=-1\) و \(\large x_2=3\) و محور \(\large y\) را در نقطهی \(\large (0,2)\) قطع کرده است. حال کافی است در معادله سهمی جایگذاری را به صورت زیر انجام دهیم:
\[\large{y=a(x+1)(x-3)}\]
با ضرب پرانتزها در هم (یا استفاده از اتحاد یک جمله مشترک) و ساده کردن آنها به معادلهی زیر میرسیم:
\[\large{y=ax^2-2ax-3a}\]
در این مرحله عرض از مبدأ یعنی نقطه \(\large (0,2)\) را در معادله بالا جایگذاری میکنیم تا مقدار مجهول \(\large a\) بهدست آید:
\[\large{2=a(0)^2-2a(0)-3a}\]
با حل این معادله به دست میآوریم:
\[\large{a=\frac{-2}{3}}\]
چه مقاله کاربردی و حرفه ای،ایول دارید خانم نقوی نیا👌👏
ممنونم از توجه شما زنده باشید.
کاملا عالی و مفید.
درود بر شما بانوی عزیز.
سپاس بابت همراهی شما. زنده باشید.