فرمولهای مهم مثلثات
فرمولهای مهم مثلثات در حل مسائل و روابط مثلثاتی بسیار مورد استفاده قرار میگیرند.
در این مقاله پرکاربردترین فرمولهای مثلثات جمع آوری شده و در اختیار کاربران عزیز قرار میگیرد.
نسبتهای مثلثاتی یعنی tan ،cos ،sin و cot در مثلث قائمالزاویه بهصورت زیر تعریف میشوند:

باید به این نکته مهم توجه داشته باشیم که در هر مثلث قائمالزاویه مانند مثلث شکل بالا، رابطهی فیثاغورس (فیثاغورث) به صورت زیر برقرار است:
\[\Large{b^2=a^2+c^2}\]
همچنین میدانیم اگر دو زاویه مانند \(\Large \alpha\) و \(\Large \beta\) متمم یکدیگر باشند (یعنی مجموع آنها برابر با 90 درجه باشد)، داریم:
\[\Large{sin\ \alpha=cos\ \beta\qquad , \qquad sin\ \beta=cos\ \alpha}\]
\[\Large{tan\ \alpha=cot\ \beta\qquad , \qquad tan\ \beta=cot\ \alpha}\]
بهعنوان مثال برای دو زاویهی \(\Large \alpha=70\) و \(\Large \beta=20\) از آنجاکه \(\Large \alpha\) و \(\Large \beta\) متمم یکدیگرند لذا:
\[\Large{sin\ 70=cos\ 20\qquad , \qquad sin\ 20=cos\ 70}\]
\[\Large{tan\ 70=cot\ 20\qquad , \qquad tan\ 20=cot\ 70}\]
آنچه در این مقاله میخوانید:
مثلثات
قاعده کسینوس
قاعده سینوس
نسبتهای مثلثاتی
فرمولهای مثلثاتی
مثلث قائمالزاویه
وتر
فرمولهای مثلثاتی مهم و پایهای
\[\Large{\qquad tan\ \alpha=\frac{sin\ \alpha}{cos\ \alpha}\qquad , \qquad \qquad cot\ \alpha=\frac{cos\ \alpha}{sin\ \alpha}}\]
پرکاربردترین فرمولهای مثلثات (روابط بین نسبتهای مثلثاتی)
1. فرمول رابطه بین سینوس و کسینوس
\[\Large{sin^2\ \alpha+ cos^2\ \alpha=1}\]
از فرمول قبل دو فرمول مهم دیگر برای محاسبهی سینوس و کسینوس بهصورت زیر بهدست میآید. کافیست یکبار \(\Large sin^2\ \alpha\) و بار دیگر \(\Large cos^2\ \alpha\) را به سمت راست معادله منتقل کنیم و سپس از طرفین ریشهی دوم بگیریم:
\[\Large{\quad sin^2\ \alpha=1-\ cos^2 \alpha\quad⇒\quad sin\ \alpha=±\sqrt{1-cos^2 \ \alpha}}\]
\[\Large{\quad cos^2\ \alpha=1-\ sin^2 \alpha\quad⇒\quad cos\ \alpha=±\sqrt{1-sin^2 \ \alpha}}\]
حال با توجه به اینکه \(\Large \alpha\) در کدام ناحیهی مثلثاتی واقع شده است میتوان علامت مثبت یا منفی را برای سینوس یا کسینوس در نظر گرفت.
2. فرمول رابطه بین تانژانت و کتانژانت
\[\Large{tan\ \alpha\times cot\ \alpha=1}\]
از فرمول بالا دو رابطهی مهم دیگر بهصورت زیر بهدست میآید:
\[\Large{\qquad tan\ \alpha=\frac{1}{cot\ \alpha}\qquad , \qquad \qquad cot\ \alpha=\frac{1}{tan\ \alpha}}\]
3. فرمول رابطه بین تانژانت و کسینوس
\[\Large{1+tan^2\ \ \alpha= \frac{1}{cos^2\ \ \alpha}}\]
اگر طرفین رابطهی بالا را معکوس کنیم داریم:
\[\Large{cos^2\ \ \alpha= \frac{1}{1+tan^2\ \ \alpha}}\]
4. فرمول رابطه بین کتانژانت و سینوس
\[\Large{1+cot^2\ \alpha= \frac{1}{sin^2\ \alpha}}\]
با معکوس کردن طرفین رابطهی بالا داریم:
\[\Large{sin^2\ \alpha= \frac{1}{1+cot^2\ \alpha}}\]
مثال 1) اگر \(\Large tan\ \ \alpha=3\) و \(\Large \alpha\) در ربع سوم مثلثاتی واقع باشد، بقیهی نسبتهای مثلثاتی زاویهی \(\Large \alpha\) را بهدست آورید.
حل: باید بهدنبال نسبتهای \(\Large sin\ \alpha\) ، \(\Large cos\ \alpha\) و \(\Large cot\ \alpha\) باشیم. سادهترین راهحل استفاده از فرمول 3 یعنی رابطهی بین تانژانت و کسینوس است. برای این کار بهصورت زیر عمل میکنیم:
\[\Large{1+tan^2\ \alpha= \frac{1}{cos^2\ \alpha}}\]
\[\Large{1+3^2= \frac{1}{cos^2\ \alpha}}\]
طرفین را معکوس میکنیم:
\[\Large{cos^2\ \alpha= \frac{1}{1+9}=\frac{1}{10}}\]
\[\Large{cos\ \alpha=±\sqrt{\frac{1}{10}}=±\frac{1}{\sqrt{10}}}\]
از آنجاکه \(\Large \alpha\) در ربع سوم قرار دارد و در این ناحیه کسینوس منفی است لذا داریم:
\[\Large{cos\ \alpha=-\frac{1}{\sqrt{10}}}\]
برای یافتن سینوس به سراغ فرمول 1 میرویم:
\[\Large{ sin\ \alpha=±\sqrt{1-cos^2\ \alpha}=±\sqrt{1-\frac{1}{10}}=±\sqrt{\frac{9}{10}}}\]
در ربع سوم سینوس منفی است، لذا:
\[\Large{sin\ \alpha=-\frac{3}{\sqrt{10}}}\]
از فرمول 2 مقدار کتانژانت را که همعلامت با تانژانت و معکوس آن است محاسبه میکنیم:
\[\Large{cot\ \ \alpha=\frac{1}{tan \alpha}=\frac{1}{3}}\]
مثال 2) اگر \(\Large cot \ \beta=-\frac{1}{4}\) و \(\Large \beta\) واقع در ربع دوم مثلثاتی باشد، بقیهی نسبتهای مثلثاتی زاویهی \(\Large \beta\) را بهدست آورید.
حل: برای محاسبهی نسبتهای \(\Large sin \ \beta\) ، \(\Large cos\ \beta\) و \(\Large tan \ \beta\) ابتدا به سراغ فرمول 4 میرویم:
\[\Large{1+cot^2\ \beta= \frac{1}{sin^2\ \beta}}\]
\[\Large{1+(-\frac{1}{4})^2= \frac{1}{sin^2\ \beta}}\]
طرفین را معکوس میکنیم:
\[\Large{sin^2\ \beta= \frac{1}{1+\frac{1}{16}}=\frac{1}{\frac{17}{16}}=\frac{16}{17}}\]
\[\Large{sin\ \beta=±\sqrt{\frac{16}{17}}=±\frac{4}{\sqrt{17}}}\]
\(\Large \beta\) در ناحیهی دوم قرار دارد و در این ناحیه سینوس مثبت است. پس:
\[\Large{sin\ \beta=\frac{4}{\sqrt{17}}}\]
برای محاسبهی کسینوس از فرمول 1 استفاده میکنیم:
\[\Large{cos\ \beta=±\sqrt{1-\ \frac{16}{17}}=±\sqrt{\frac{1}{17}}}\]
در ربع دوم کسینوس منفی است، لذا:
\[\Large{cos\ \beta=-\frac{1}{\sqrt{17}}}\]
از فرمول 2 مقدار تانژانت را که همعلامت با کتانژانت و معکوس آن است بهدست میآوریم:
\[\Large{tan\ \beta=\frac{1}{cot\ \beta}=\frac{1}{-\frac{1}{4}}=-4}\]
یکی از بهترین کارهایی که میشه انجام داد، کمک به افزایش آگاهی و دانش دیگران هست. مثلا میتونید کتابهای درسی و کمک درسی که مربوط به سالهای گذشته هستن و نیازی بهشون ندارید رو به دانشآموزانی که توانایی خرید این کتابها رو ندارن تقدیم کنید.
در هر شهری که زندگی میکنید مراکزی برای دریافت کتابها وجود دارن. کافیه با یک سرچ ساده در گوگل اونها رو پیدا کنید.
همین حالا در آزمون آنلاین مثلثات دهم شرکت کنید.
تمرین) \(\Large \beta\) در ربع چهارم مثلثاتی قرار دارد و \(\Large cos \beta=\frac{1}{3}\) است. بقیهی نسبتهای مثلثاتی زاویهی \(\Large \beta\) را بهدست آورید.
در حل تمرین اشکال داشتید؟ پس بیاید اینجا رو ببینید:
نسبتهای مثلثاتی زوایای بیشتر از \(\Large \alpha\)
\[\Large{ sin(\pi+\alpha)=-sin \alpha \qquad \qquad sin(\pi-\alpha)=sin\alpha}\]
\[\Large{ sin(2\pi+\alpha)=sin \alpha \qquad \qquad sin(2\pi-\alpha)=-sin\alpha}\]
\[\Large{ cos(\pi+\alpha)=-cos \alpha \qquad \qquad cos(\pi-\alpha)=-cos\alpha}\]
\[\Large{ cos(2\pi+\alpha)=cos \alpha \qquad \qquad sin(2\pi-\alpha)=cos\alpha}\]
مثال 3) نسبتهای مثلثاتی زاویهی \(\Large \ 135^°\) را محاسبه کنید.
حل: میدانیم \(\Large \ 135^°=180^°-45°\) . حال اگر زاویهها را بر حسب رادیان نمایش دهیم خواهیم داشت:
\[\Large{180^°=\pi \qquad \qquad45^°=\frac{\pi}{4}}\]
با استفاده از فرمولهای بالا، یعنی:
\[\Large{sin(\pi-\alpha)=sin\ \alpha}\]
و با فرض \(\Large \ \alpha=45^°\) میتوانیم بنویسیم:
\[\Large{sin\ 135^°=sin(180^°-45^°)}\]
\[\Large{sin\ 135^°=sin(\pi-\frac{\pi}{4})=sin\ \frac{\pi}{4}}\]
میدانیم \(\Large sin\ 45^°=\frac{\sqrt{2}}{2}\) پس:
\[\Large{sin\ 135^°=\frac{\sqrt{2}}{2}}\]
همچنین:
\[\Large{cos(\pi-\alpha)=-cos\ \alpha}\]
در نتیجه:
\[\Large{cos\ 135^°=cos(\pi-\frac{\pi}{4})=-cos\ \frac{\pi}{4}}\]
از طرفی:
میدانیم \(\Large cos\ 45^°=\frac{\sqrt{2}}{2}\) پس:
\[\Large{cos\ 135^°=-\frac{\sqrt{2}}{2}}\]
محاسبهی بقیهی نسبتها:
\[\Large{tan\ 135^°=\frac{sin\ 135^°}{cos\ 135^°}}\]
\[\Large{=\frac{\frac{\sqrt{2}}{2}}{-\frac{\sqrt{2}}{2}}}\]
\[\Large{tan\ 135^°=-1}\]
از طرفی:
\[\Large{cot\ 135^°=\frac{1}{tan\ 135^°}=\frac{1}{-1}=-1}\]
نسبتهای مثلثاتی دوبرابر زاویه (دو برابر کمان)
\[\Large{ sin\ \ 2\alpha=2sin \ \alpha\ cos \ \alpha\ }\ \]
برای \(\Large cos\ 2\alpha\) سه فرمول داریم:
\[\Large{ cos\ 2\alpha=cos^2\alpha-sin^2\alpha}\]
\[\Large{ cos\ 2\alpha=2cos^2\alpha-1}\]
\[\Large{ cos\ 2\alpha=1-2sin^2\ \alpha}\]
نسبتهای مثلثاتی نصف زاویه (نصف کمان)
\[\Large{ sin^2\ \frac{\alpha}{2}=\frac{1-cos\ \alpha}{2} }\]
\[\Large{ cos^2\ \frac{\alpha}{2}=\frac{1+cos\ \alpha}{2} }\]
تانژانت و کتانژانت 15 درجه رو چطور حساب کنیم؟؟ شما بگید! در بخش نظرات!
مثال 4) با دانستن نسبتهای مثلثاتی 30 درجه قصد داریم نسبتهای مثلثاتی 15 درجه را بهدست آوریم.
حل: از آنجا که 15 نصف 30 است برای محاسبهی نسبتهای مثلثاتی 15 درجه کافیست از فرمول نصف کمان استفاده کنیم:
\[\Large{ sin^2\ \frac{\alpha}{2}=\frac{1-cos\ \alpha}{2} }\]
\[\Large{ sin^2\ 15=\frac{1-cos\ 30}{2} =\frac{1-\frac{\sqrt{3}}{2}}{2}}\]
\[\Large{sin^2\ 15=\frac{\frac{2-\sqrt{3}}{2}}{2}=\frac{2-\sqrt{3}}{4} }\]
حال کافیست از طرفین جذر بگیریم:
\[\Large{ sin\ 15=±\sqrt{\frac{2-\sqrt{3}}{4}}}\]
میدانیم زاویهی 15 درجه در ربع اول واقع است و لذا تمام مقادیر نسبتهای مثلثاتی مربوط به آن مثبت است. لذا:
\[\Large{ sin\ 15=\sqrt{\frac{2-\sqrt{3}}{4}}=\frac{\sqrt{2-\sqrt{3}}}{2}}\]
برای محاسبه کسینوس 15 درجه میتوان نوشت:
\[\Large{cos\alpha=±\sqrt{1-sin^2 \alpha}}\]
\[\Large{cos\ 15=±\sqrt{1-sin^2 15}}\]
\[\Large{cos\ 15=\sqrt{1-\frac{2-\sqrt{3}}{4}}}\]
\[\Large{=\sqrt{\frac{4-2+\sqrt{3}}{4}}}\]
\[\Large{=\sqrt{\frac{2+\sqrt{3}}{4}}}\]
\[\Large{cos\ 15=\frac{\sqrt{2+\sqrt{3}}}{2}}\]
نسبتهای مثلثاتی زوایای متمم
\[\Large{ sin(\frac{\pi}{2}+\alpha)=cos\ \alpha \qquad \qquad sin(\frac{\pi}{2}-\alpha)=cos\ \alpha}\]
\[\Large{ cos(\frac{\pi}{2}+\alpha)=-sin\ \alpha \qquad \qquad cos(\frac{\pi}{2}-\alpha)=sin\ \alpha}\]
\[\Large{ sin(\frac{3\pi}{2}+\alpha)=-cos\ \alpha \qquad \qquad sin(\frac{3\pi}{2}-\alpha)=-cos\ \alpha}\]
\[\Large{ cos(\frac{3\pi}{2}+\alpha)=sin\ \alpha \qquad \qquad cos(\frac{3\pi}{2}-\alpha)=-sin\ \alpha}\]
نسبتهای مثلثاتی زاویه \(\Large -\alpha\)
\[\Large{sin(-\alpha)=-sin\ \alpha\qquad , \qquad \qquad cos(-\alpha)=cos\ \alpha}\]
\[\Large{tan(-\alpha)=-tan\ \alpha\qquad , \qquad \qquad cot(-\alpha)=-cot\ \alpha}\]
فرمول مساحت مثلث با سینوس

\[\Large{ S_{ABC}=\frac{1}{2}\ b\ c\ sin\ A}\]
\[\Large{ S_{ABC}=\frac{1}{2}\ a\ b\ sin\ C}\]
\[\Large{ S_{ABC}=\frac{1}{2}\ a\ c\ sin\ B}\]
برای محاسبهی مساحت مثلث بالا ( \(\large S_{ABC}\)) میتوان از هریک از سه فرمول استفاده کرد. با توجه به اطلاعات مسألهای که با آن مواجه هستید میتوان یکی از فرمولها را انتخاب کرد. بدیهی است از آنجاکه یک شکل تنها میتواند یک مقدار برای مساحت داشته باشد، لذا جواب هرسه فرمول بالا با هم برابر است.
مثال 5) مساحت مثلث زیر را بهدست آورید.
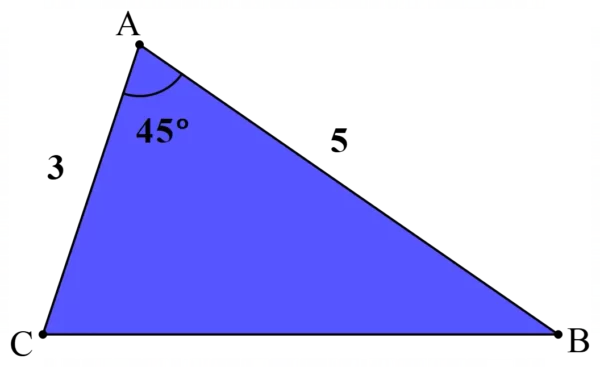
حل: با استفاده از رابطه فرمول مساحت مثلث با سینوس میتوانیم بنویسیم:
\[\Large{ S_{ABC}=\frac{1}{2}\ AC\ \times\ \ AB\ sin\ A}\]
\[\Large{ S_{ABC}=\frac{1}{2}\ \times\ \ 3\ \times\ \ 5\ sin\ (45)}\]
\[\Large{ =\frac{1}{2}\ \times\ \ 3\ \times\ \ 5\ \times\ \frac{\sqrt{2}}{2}}\]
\[\Large{ S_{ABC}=\frac{15}{4}\ \sqrt{2}}\]
این مقاله را با دیگران به اشتراک بگذارید:
قاعده سینوس ها و قاعده کسینوس ها

قاعده سینوس ها:
\[\Large{\frac{sin\ A}{a}=\frac{sin\ B}{b}=\frac{sin\ C}{c}}\]
قاعده کسینوس ها:
\[\Large{b^2=c^2+a^2-2\ ac\ cos\ B}\]
\[\Large{a^2=c^2+b^2-2\ bc\ cos\ A}\]
\[\Large{c^2=b^2+a^2-2\ ab\ cos\ C}\]
