تعیین علامت ریاضی دهم
تعیین علامت ریاضی دهم در فصل 4 ریاضی 1 مورد بررسی قرار میگیرد. تعیین علامت بهطور ویژه برای حل نامعادله ها بهکار میرود.
هدف از حل یک نامعادله یافتن یک مجموعه جواب برای نامعادله است. تعیین علامت عبارت های جبری به صورت: تعیین علامت عبارت های درجه اول و تعیین علامت عبارت های درجه دوم تفکیک میشود.
برای یادگیری این مبحث ابتدا باید مباحث زیر را به خوبی یاد بگیرید و مقالات آن را حتما با دقت مطالعه نمایید:
آنچه در این مقاله میخوانید:
تعیین علامت عبارت های درجه اول
برای تعیین علامت عبارت های درجه اول مانند \(\large ax+b\) ابتدا لازم است ریشه عبارت را تعیین کنیم. جهت تعیین ریشه باید عبارت را مساوی صفر قرار دهیم و \(\large x\)ی که بهدست میآید ریشهی مورد نظر است.
\[\large{ax+b=0}\]
\[\large{ax=-b}\]
\[\large{x=-\frac{b}{a}}\]
حال عبارت جبری را مطابق جدول زیر تعیین علامت میکنیم:

مثال 1) عبارت \(\large P=3x-3\) را تعیین علامت کنید.
حل: ابتدا عبارت جبری مورد نظر را برابر با صفر قرار میدهیم تا ریشهی آن را بهدست آوریم:
\[\large{3x-3=0}\]
\[\large{3x=3}\]
\[\large{x=\frac{3}{3}=1}\]
حال جدول تعیین علامت را بهصورت زیر رسم میکنیم (توجه داریم که در این مثال ضریب \(\large x\) یعنی \(\large a\) برابر است با 3. یعنی علامت \(\large a\) مثبت است):

یکی از بهترین کارهایی که میشه انجام داد، کمک به افزایش آگاهی و دانش دیگران هست. مثلا میتونید کتابهای درسی و کمک درسی که مربوط به سالهای گذشته هستن و نیازی بهشون ندارید رو به دانشآموزانی که توانایی خرید این کتابها رو ندارن تقدیم کنید.
در هر شهری که زندگی میکنید مراکزی برای دریافت کتابها وجود دارن. کافیه با یک سرچ ساده در گوگل اونها رو پیدا کنید.
تعیین علامت عبارت های درجه دوم
جهت تعیین علامت عبارت های درجه دوم که بهصورت کلی \(\large y=ax^2+bx+c\) هستند نیز ابتدا باید ریشهی عبارت مورد نظر را تعیین کنیم.
همانطور که در مقالهی روش های حل معادله درجه دو بیان کردیم، یکی از راههای یافتن جواب های معادله درجه دوم استفاده از فرمول کلی یا روش دلتا است.
لذا برای حل معادله درجه 2 مورد نظر ابتدا آن را مساوی صفر قرار میدهیم و دلتا را محاسبه میکنیم. میدانیم برای \(\largeΔ\) سه حالت رخ میدهد:
- \(\largeΔ>0\)، در این حالت معادله دو ریشهی حقیقی و متمایز دارد. این دو ریشه با استفاده از فرمولهای زیر بهدست میآیند:
\[\large\begin{cases}x_1=\frac{-b+\sqrt{Δ}}{2a}\\[0.5cm] \\x_2=\frac{-b-\sqrt{Δ}}{2a}\ \end{cases}\]
- \(\largeΔ=0\)، در اینصورت معادلهی درجه دو یک ریشهی مضاعف دارد که فرمول محاسبهی آن بهصورت زیر است:
\[\large{x=\frac{-b}{2a}}\]
- \(\largeΔ<0\)، در این حالت معادله ریشهی حقیقی ندارد.
برای هر کدام از این سه حالت جدول تعیین علامت منحصربهفردی وجود دارد. در ادامه میتوانید جداول و مثالهای مربوط به هر کدام از حالتها را مشاهده نمایید:
همین حالا در آزمون آنلاین تعیین علامت دهم شرکت کنید.
الف) \(\largeΔ>0\) : (با فرض \(\large x_1<x_2\))

مثال 2) عبارت \(\large A=-5x^2+4x+1\) را تعیین علامت کنید.
حل: ابتدا قرار میدهیم: \(\large A=0\). یعنی \(\large -5x^2+4x+1=0\) و ریشهی آن را از طریق روش دلتا به دست میآوریم:
\[\large{Δ=b^2-4ac}\]
\[\large{Δ=4^2-4(-5)(1)}\]
\[\large{=16+20=36>0}\]
از آنجایی که \(\large Δ>0\) است لذا معادله دارای دو ریشهی حقیقی متمایز است که بهصورت زیر محاسبه میشود:
\[\large\begin{cases}x_1=\frac{-b+\sqrt{Δ}}{2a}=\frac{-4+\sqrt{36}}{2(-5)}=\frac{-1}{5}\\[0.5cm] \\x_2=\frac{-b-\sqrt{Δ}}{2a}=\frac{-4-\sqrt{36}}{2(-5)}=\frac{-10}{-10}=1\ \end{cases}\]
حال جدول تعیین علامت را مطابق شکل زیر رسم میکنیم:

ب) \(\largeΔ=0\) :

مثال 3) عبارت \(\large B=x^2-8x+16\) را تعیین علامت کنید.
حل: ابتدا عبارت \(\large B\) را مساوی صفر قرار داده و ریشهی آن را از روش \(\large Δ\) به دست میآوریم:
\[\large{Δ=b^2-4ac}\]
\[\large{Δ=(-8)^2-4(1)(16)}\]
\[\large{=64-64=0}\]
از آنجایی که \(\large Δ=0\) است لذا معادله دارای یک ریشهی مضاعف است که بهصورت زیر محاسبه میشود:
\[\large{x=\frac{-b}{2a}=\frac{8}{2}=4}\]
سپس جدول تعیین علامت را بهصورت زیر رسم میکنیم:
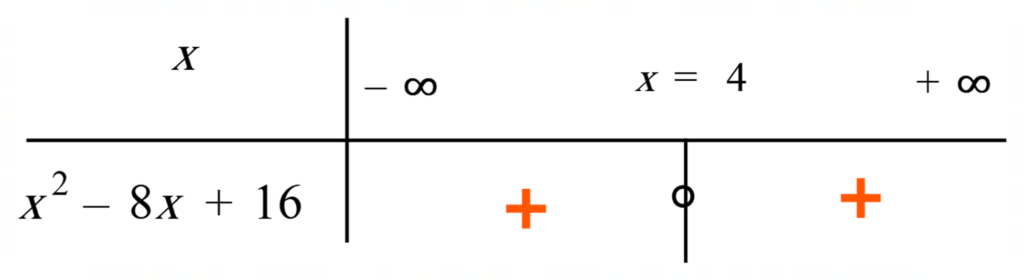
ج) \(\largeΔ<0\) :

مثال 4) عبارت \(\large P=x^2+3x+4\) را تعیین علامت کنید.
حل: ابتدا ریشهی عبارت \(\large P\) را از روش \(\large Δ\) به دست میآوریم:
\[\large{Δ=b^2-4ac}\]
\[\large{Δ=3^2-4(1)(4)}\]
\[\large{=9-16=-7<0}\]
\(\large Δ<0\) است بنابراین معادله ریشهی حقیقی ندارد. حال جدول تعیین علامت را بهصورت زیر رسم میکنیم:
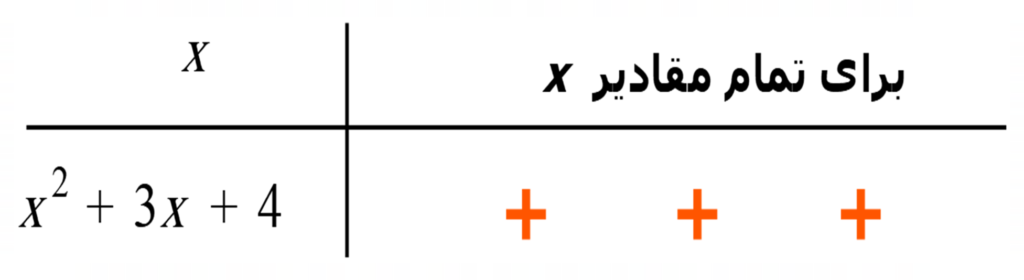
این مقاله را با دیگران به اشتراک بگذارید:
حل نامعادله ها با استفاده از تعیین علامت
هدف از حل یک معادله یافتن جوابهایی برای آن است. یک معادله از درجهی \(\large n\) حداکثر \(\large n\) جواب دارد. یعنی میتواند صفر (یعنی اصلا جواب ندارد)، یک، دو، سه، … یا \(\large n\) جواب داشته باشد. اما در حل نامعادله ها بهدنبال یافتن یک محدوده جواب یا مجموعه جواب یا یک بازه از جوابها برای نامعادله هستیم.
این امکان وجود دارد که مجموعه جواب نامعادله تهی باشد. بهعبارتی نامعادله در هیچ محدودهای تعریف نشده است. یا میتوان گفت هیچ مقداری برای \(\large x\) وجود ندارد که بهازای آن نامعادله موردنظر برقرار باشد.
مجموعه جواب نامعادله
- مجموعه جواب نامعادله درجه اول
برای حل نامعادله های درجه اول، هم میتوان بهطور مستقیم نامعادله را حل کرد و هم از طریق تعیین علامت. نکتهی بسیار مهمی که در حل نامعادله باید به آن توجه داشته باشیم این است که:
اگر طرفین یک نامعادله را در یک عدد منفی ضرب یا بر یک عدد منفی تقسیم کنیم جهت نامعادله برعکس میشود.
روش اول (از راه مستقیم)
در این روش کافیست مانند روش حل معادله درجه اول عمل کنیم. برای درک بهتر لطفا به مثال زیر دقت کنید:
مثال 5) مجموعه جواب نامعادلهی \(\large -2x+1<4\) را بهدست آورید.
حل: ابتدا اعداد را به سمت راست نامعادله منتقل میکنیم (مانند حل معادله درجه یک):
\[\large{-2x<4-1}\]
\[\large{-2x<3}\]
حال طرفین نامعادله را بر ضریب \(\large x\) یعنی \(\large-2\) تقسیم میکنیم. باید به این نکته دقت کنیم از آنجا که \(\large -2\) یک عدد منفی است زمانیکه دو طرف نامعادله را بر آن تقسیم کنیم جهت نامعادله برعکس میشود. یعنی،
\[\large{x>-\frac{3}{2}}\]
در واقع مجموعه جواب نامعادله برابر است با: \(\large x\)های بزرگتر از \(\large -\frac{3}{2}\) . اگر بخواهیم محدوده جواب نامعادله را بهصورت بازه نمایش دهیم مینویسیم:
\[\large{x ∈ (-\frac{3}{2},+∞)}\]
همچنین میتوان مجموعه جواب نامعادله موردنظر را روی محور اعداد حقیقی نیز نمایش داد:

روش دوم (از طریق تعیین علامت)
در این روش ابتدا همهی اجزاء نامعادله را به سمت چپ منتقل میکنیم تا طرف دیگر برابر صفر شود:
\[\large{-2x+1-4<0}\]
\[\large{-2x-3<0}\]
حال کافیست عبارت درجه اول \(\large A=-2x-3\) را تعیین علامت کنیم. میدانیم اولین گام در تعیین علامت تعیین ریشهی عبارت موردنظر است:
\[\large{-2x-3=0}\]
\[\large{x=-\frac{3}{2}}\]
سپس جدول تعیین علامت را بهصورت زیر رسم میکنیم:

برای یافتن مجموعه جواب نامعادله \(\large -2x-3<0\) توجه داریم که باید بازهای را در نظر بگیریم که عبارت \(\large -2x-3\) کوچکتر از صفر باشد. با مشاهده جدول تعیین علامت درمییابیم بازهی مورد نظر عبارت است از:
\[\large{x ∈ (-\frac{3}{2},+∞)}\]
تعیین علامت عبارت های خاص
برای تعیین علامت بعضی عبارت های خاص مانند عبارت های قدرمطلقی و درجه فرد بزرگتر از 1 و عبارتهای کسری باید بعضی نکات خاص را در نظر داشته باشیم. در ادامه میتوانید آموزش تعیین علامت این نوع عبارتها را دنبال نمایید.
تعیین علامت عبارت های قدرمطلقی
همانطور که میدانید تابع قدرمطلق همیشه مثبت است. لذا در روند تعیین علامت عبارت های قدرمطلقی پس از تعیین ریشهی عبارت داخل مطلق جدول تعیین علامت را رسم میکنیم.
عبارت داده شده همهجا مثبت است و فقط در ریشهی بهدست آمده صفر میشود. برای درک مطلب لطفا به مثال بعدی توجه کنید.
مثال 6) عبارت \(\large P=|x-2|\) را تعیین علامت کنید.
حل: ابتدا ریشهی عبارت داخل قدرمطلق را بهدست میآوریم:
\[\large{x-2=0}\]
\[\large{x=2}\]
جدول تعیین علامت را رسم میکنیم:

تعیین علامت عبارت های درجه فرد بزرگتر از یک
جهت تعیین علامت عبارت های درجه 3، 5، 7 و … با آنها مانند درجه اول رفتار میکنیم. یعنی فرض میکنیم توان آنها برابر یک است. در ادامه میتوانید فیلم آموزش این مطلب را مشاهده فرمایید.
تعیین علامت عبارت های کسری
برای این منظور ابتدا بهصورت مجزا ریشهی صورت و مخرج را بهدست میآوریم. سپس جدول تعیین علامت را به گونهای رسم میکنیم که در هر ردیف تمام عاملهای مجزای صورت و مخرج نوشته شود.
در سطر آخر عبارت اصلی را که قرار است تعیین علامت شود مینویسیم. ریشههای مربوط به هر عبارت را در جلوی آن عبارت صفر میکنیم. باید به این نکته توجه داشت که صفر ریشهی مخرج را جلوی آن نمینویسیم. چون مخرج نباید صفر شود. بهجای عدد صفر علامت \(\large∞\) را قرار میدهیم.
برای درک بیشتر این مبحث لطفا به مثال زیر دقت کنید:
مثال 7) عبارت \(\large A=\frac{2x-3}{x+1}\) را تعیین علامت کنید.
حل: ابتدا ریشهی صورت و مخرج را تعیین میکنیم.
ریشهی صورت:
\[\large{2x-3=0}\]
\[\large{x=\frac{3}{2}}\]
ریشهی مخرج:
\[\large{x+1=0=}\]
\[\large{x=-1}\]
جدول تعیین علامت :

توجه داریم که برای هر سطر جدول تعیین علامت مربوط به عبارتهای کسری، تمام مواردی را که در بخش مربوط به تعیین علامت عبارت های درجه اول و درجه دوم بیان کردیم برقرارند.
مثلا در سطر اول جدول بالا میبینیم که برای عبارت \(\large 2x-3\) قبل از ریشه یعنی \(\large \frac{3}{2}\) مخالف علامت \(\large a=2\) یعنی منفی است و بعد ریشه موافق علامت \(\large a\) یعنی مثبت است.
همچنین در سطر پایانی برای تعیین علامت نهایی کسر موردنظر کافیست علامتهایی را که بالای آن قرار دارند را در هم ضرب کنیم. مثلا اولین علامت که مثبت است از ضرب دو علامت منفی یا اصطلاحا منفی در منفی=مثبت بهدست آمده است.
در ویدئوی زیر مثالهایی حل شدهاند که برای درک کامل این مبحث حتما آن را تا پایان مشاهده بفرمایید.
نکته بسیار مهم و کنکوری
دستهای از سؤالات بسیار مهم و پرتکرار در امتحانات و بهویژه در تست های کنکور سراسری بهصورت زیر بیان میشوند:
- محدودهی \(\large m\) را بهگونهای بهدست آورید که تابع \(\large y=mx^2+2mx-m+1\) همواره بالای محور \(\large x\)ها باشد.
- بهازای چه مقادیری از \(\large k\) تابع \(\large y=(k-1)x^2-4x+2k-1\) همواره زیر محور \(\large x\)ها است؟
برای حل سؤالاتی از این قبیل باید نکتههای خاصی را بدانید که در ویدئوی آموزشی زیر به آنها اشاره خواهم کرد. پس لطفا این فیلم را تا پایان مشاهده بفرمایید.
عالی
ممنون از توجه و همراهی شما